Physics behind Heavy Stars - 1
I recently bought the book “Brief Answers to Big Questions” by Stephen Hawking, and it re-sparked my enthusiasm for physics. It’s been a long time since I’ve written something in Physics, and I thought of making this blackhole series where I’ll explain the blackhole formation and its math as easily as possible. So, we start with defining the formation of stars in this blog.
Part 1: Becoming a Protostar
The story of any star begins in the vast, cold interstellar space, specifically within Giant Molecular Clouds (GMCs). These are colossal reservoirs of gas (primarily hydrogen and helium) and dust, spanning hundreds or thousands of light-years and containing hundreds of thousands, sometimes millions, of solar masses of material. Within these clouds, density fluctuations and turbulent motions exist. The fundamental force that initiates star formation is gravity.

The Orion Nebula (Messier 42) is such a cloud composed primarily of hydrogen gas, dust, and young stars, with a total mass of about 2,000 solar masses. It lies approximately 1,344 light-years from Earth and spans about 24 light-years across.
Every particle in the cloud exerts a gravitational pull on every other particle. In most parts of the cloud, the outward pressure arising from the thermal motion of the gas particles and turbulence is sufficient to resist the inward pull of gravity, maintaining a state of equilibrium. However, if a region within the cloud becomes sufficiently dense or cold, gravity can begin to dominate over the internal pressure. This condition is often described by the Jeans Instability.
The Jeans Criterion gives the condition under which gravity overcomes pressure:
$$ M_J = \left( \frac{5 k_B T}{G \mu m_H} \right)^{3/2} \left( \frac{3}{4 \pi \rho_0} \right)^{1/2} $$
where
- $M_J$ is the Jeans mass,
- $T$ is the temperature,
- $\rho_0$ is the initial density,
- $\mu$ is the mean molecular weight,
- $m_H$ is the hydrogen atom mass,
- and $k_B$, $G$ are Boltzmann and Gravitational constants.
When the mass of a region exceeds the Jeans Mass, its self-gravity is strong enough to overcome the opposing pressure forces, leading to a runaway collapse. This collapse isn’t uniform; the denser clusters within the cloud collapse faster, leading to fragmentation and the formation of multiple star systems.
As a region collapses, gravitational potential energy is converted into kinetic energy, and collisions between particles heat the gas.
The gravitational energy released during collapse can be approximated as:
$$ U = -\frac{3}{5} \frac{GM^2}{R} $$
where $M$ is the mass of the core and $R$ is its radius.
The core of the collapsing region becomes increasingly dense and hot. Material from the surrounding cloud continues to fall onto this central region. Eventually, a dense, hot object forms at the center, still accreting mass from its surroundings, which forms the protostar. The physics at this stage is primarily governed by gravity and hydrodynamics, with the protostar supported temporarily by the pressure from the infalling material and its internal thermal pressure generated by the collapse itself.

As depicted, a protostar would blast powerful jets and stellar winds due to the interaction of magnetic field / accreting material from the disk.
Part 2: Becoming a Main-Sequence Star
The protostar continues to contract under its own gravity. As more mass is added and the core shrinks, the temperature and pressure at the very center continue to climb dramatically. This inward gravitational pressure is the driving force behind the increasing core conditions.
As gravitational potential energy converts to thermal energy, the virial theorem relates the average kinetic energy ($K$) and potential energy ($U$) of a bound system:
$$ 2K + U = 0 $$
This implies that as the system contracts and $U$ becomes more negative, the temperature (related to $K$) increases.
A critical threshold is reached when the core temperature becomes high enough, like millions of degrees Kelvin. At these temperatures, atomic nuclei, which are normally kept apart by their electrostatic (Coulomb) repulsion, are moving fast enough to overcome this barrier and get close enough for the strong nuclear force to take over. This is the ignition point for nuclear fusion.
The kinetic energy per particle required to overcome the Coulomb barrier can be roughly estimated by equating thermal energy with electrostatic potential energy:
$$ k_B T \gtrsim \frac{Z_1 Z_2 e^2}{4 \pi \varepsilon_0 r} $$
where
- $Z_1$ and $Z_2$ are the atomic numbers of the fusing nuclei,
- $e$ is the elementary charge, $r$ is the distance of closest approach,
- and $\varepsilon_0$ is the vacuum permittivity.
In the core, hydrogen nuclei (protons) begin to fuse together to form helium nuclei. This process releases an enormous amount of energy, primarily in the form of gamma-ray photons and neutrinos. This energy heats the surrounding plasma, increasing its thermal pressure.
The net energy released by the proton–proton chain (dominant in Sun-like stars) is:
$$ 4p \rightarrow ,^4\mathrm{He} + 2e^+ + 2\nu_e + \gamma + \text{Energy} $$
with about 26.7 MeV of energy released per reaction.
When the energy generated by nuclear fusion in the core becomes sufficient, it creates an outward pressure that perfectly balances the inward pull of gravity from the star’s immense mass. This state of perfect balance is called hydrostatic equilibrium.
Hydrostatic equilibrium is governed by the equation:
$$ \frac{dP}{dr} = -\frac{G M(r) \rho(r)}{r^2} $$
where
- $P$ is the pressure,
- $r$ is radius,
- $\rho(r)$ is density,
- and $M(r)$ is the mass enclosed within radius $r$.
A star that has achieved stable hydrogen fusion in its core and is in hydrostatic equilibrium is called a main-sequence star. This phase constitutes the majority of a star’s active lifetime.
Stars on the main sequence vary widely in mass, temperature, and luminosity. Astronomers classify them using spectral types, ordered from hottest to coolest: O, B, A, F, G, K, M. Our Sun is a G-type star. Heavy stars, the focus of this blog, belong to the O and B spectral types. They are the most massive, hottest, and most luminous stars on the main sequence.
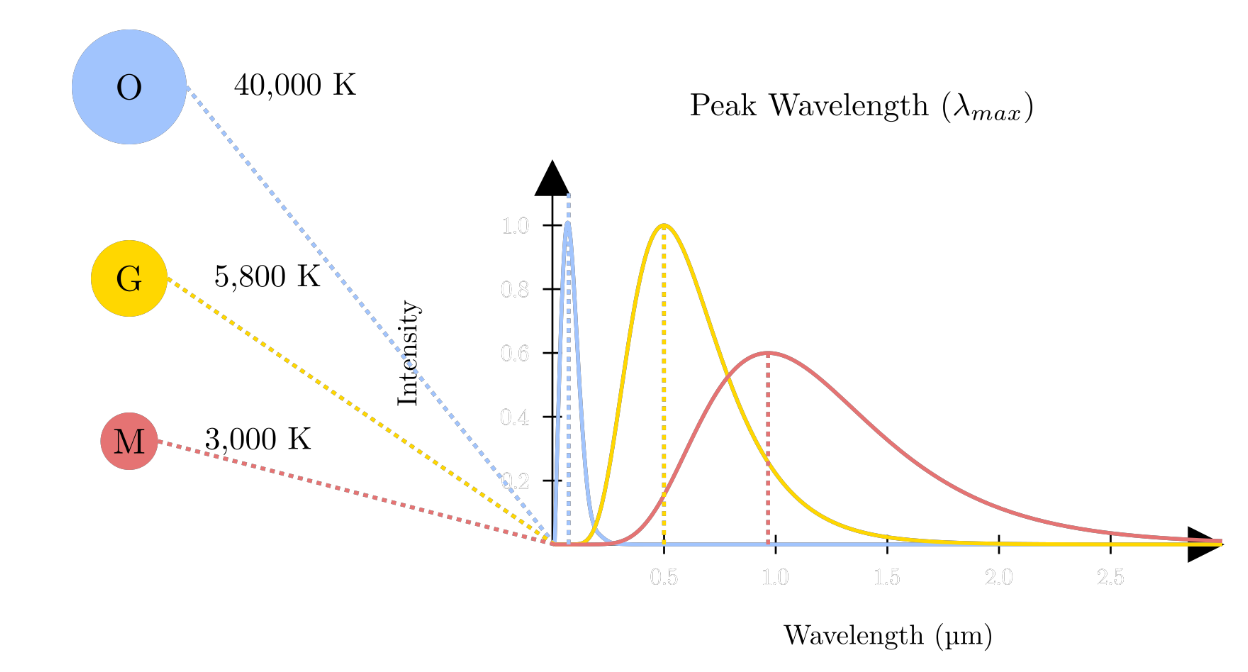
Hotter stars (O-type) peak at shorter, bluer wavelengths, while cooler stars (M-type) peak at longer, redder wavelengths as by Wien's Displacement Law for blackbody radiation.
Wien’s Displacement Law
Wien’s Displacement Law states that the wavelength $(\lambda_{\text{max}}) $ at which a blackbody emits most strongly is inversely proportional to its temperature (T). As the temperature increases, the peak emission shifts to shorter wavelengths (bluer light).
$$ \lambda_{\text{max}} = \frac{b}{T}, \quad \text{where } b = 2.898 \times 10^{-3} \text{m} \cdot \text{K} $$
Part 3: Life on the Main Sequence Stars
While all main-sequence stars fuse hydrogen into helium, the method of fusion and the rate at which it occurs differ significantly between low-mass and high-mass stars, leading to vastly different lifespans.
In lower-mass stars like our Sun, the primary fusion process is the proton-proton (p-p) chain. This is a relatively direct process where protons collide and, through a series of steps involving weak force interactions, eventually form a helium nucleus. The p-p chain is temperature-sensitive, but not dramatically so.
The simplified net reaction for the proton-proton chain is:
$$ 4p \rightarrow ,^4\mathrm{He} + 2e^+ + 2\nu_e + \gamma + 26.7,\text{MeV} $$
This chain dominates in stars with core temperatures around $10^7$ K, like the Sun.
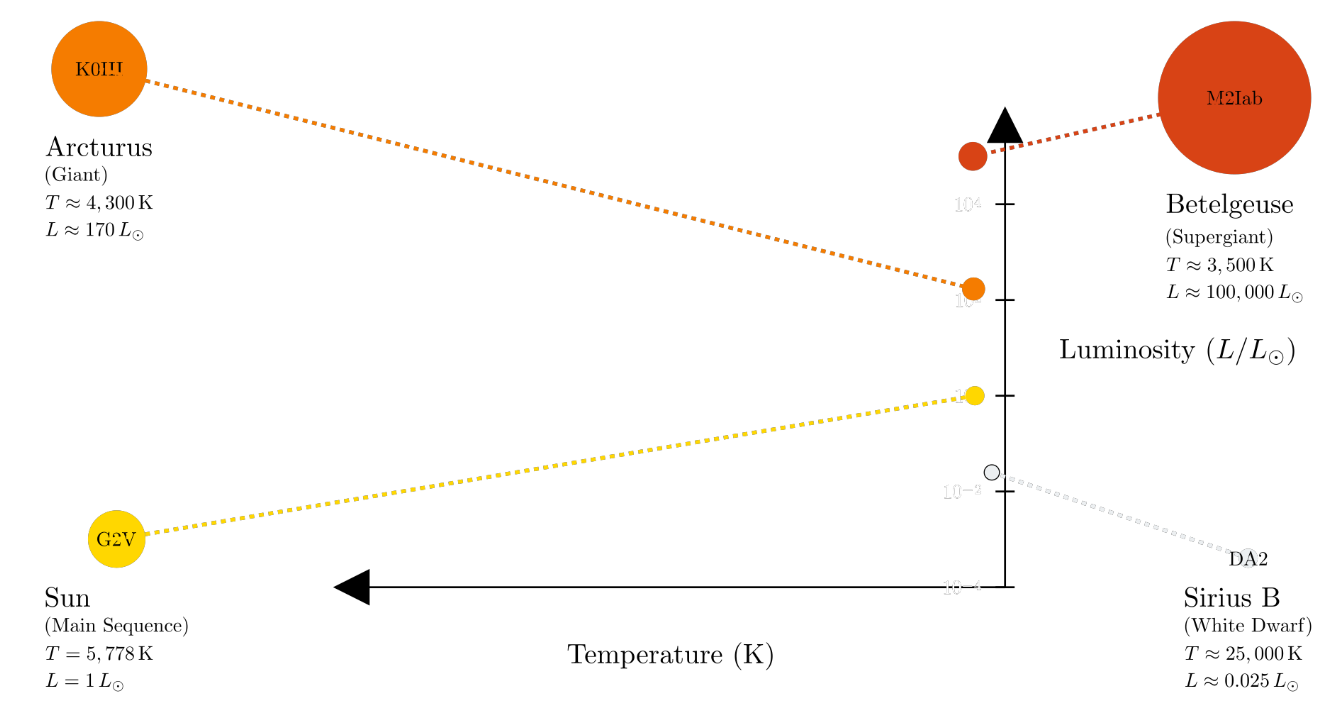
A simplified Hertzsprung-Russell (H-R) diagram, plotting stellar luminosity (Y-axis) against surface temperature (X-axis).
In the cores of massive (O and B type) stars, however, the temperatures are much higher – typically exceeding 18 million Kelvin. At these extreme temperatures, a different fusion process becomes dominant: the CNO Cycle. This is a catalytic cycle involving isotopes of Carbon (C), Nitrogen (N), and Oxygen (O) as intermediaries. These heavier nuclei act as catalysts, facilitating the fusion of hydrogen into helium without being consumed themselves (they are regenerated at the end of the cycle). The CNO cycle is far more efficient than the p-p chain at high temperatures, and its rate is extremely sensitive to temperature.
The simplified net reaction for the CNO cycle is also:
$$ 4p \rightarrow ,^4\mathrm{He} + 2e^+ + 2\nu_e + \gamma + 25,\text{MeV} $$
But the key difference lies in its temperature dependence:
$$ \text{Rate}_{\text{CNO}} \propto T^{20} $$
compared to:
$$ \text{Rate}_{\text{p-p}} \propto T^4 $$
This means even small increases in core temperature in massive stars cause fusion rates to skyrocket.
The dominance of the CNO cycle in massive stars means they burn through their hydrogen fuel at an astonishing rate. Their energy output (luminosity) is orders of magnitude higher than that of lower-mass stars.
Luminosity scales roughly with mass as:
$$ L \propto M^{3.5} $$
So a star with 10 times the mass of the Sun can be over 3,000 times more luminous.
This rapid energy generation provides the immense thermal pressure required to support the star against its correspondingly immense gravitational pull.
The consequence of this accelerated fusion rate is a dramatically shortened lifespan. While a star like our Sun will spend about 10 billion years on the main sequence, a massive O-type star might exhaust its core hydrogen in just a few million years.
Stellar lifetime scales inversely with luminosity:
$$ \tau \propto \frac{M}{L} \propto M^{-2.5} $$
Hence, more massive stars live much shorter lives.
They live fast and bright, but die young compared to their less massive counterparts. During this main-sequence phase, the star remains supported by the thermal pressure generated by the CNO-cycle fusion in its core, maintaining hydrostatic equilibrium.
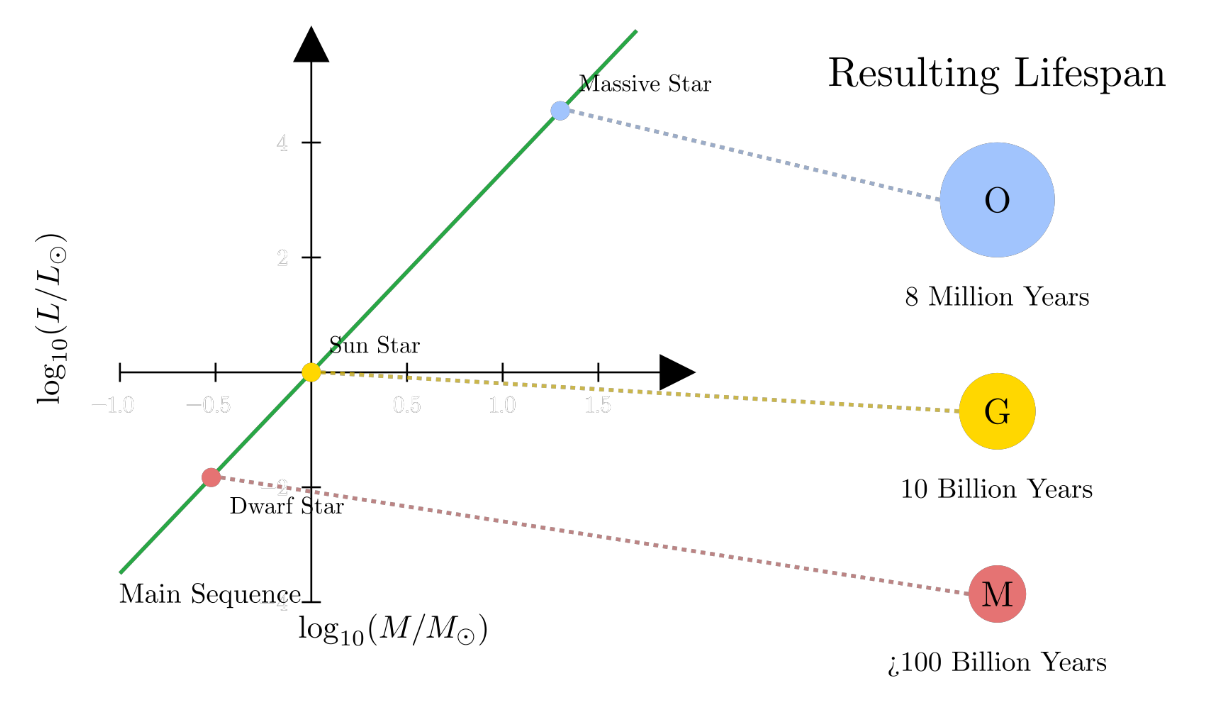
Relationship between a main-sequence star's mass, luminosity, and its resulting lifespan. Higher mass stars are significantly more luminous and, consequently, have much shorter main-sequence lifetimes. Conversely, low-mass stars are dimmer but live far longer.
Further…
What happens once a star fuses all the hydrogen in the core to helium?