type II supernova - collapse of heavy stars
Read Part 1 - Physics behind Heavy Stars
what happens once a star fuses all the hydrogen in the core to helium?
Once the hydrogen fuel in the star’s core is largely exhausted and converted into helium, nuclear fusion ceases in that central region. Without the outward thermal pressure generated by core hydrogen fusion, gravity immediately begins to win the tug-of-war. The inert helium core starts to contract under its own immense weight. This gravitational compression releases potential energy, which heats both the core itself and, crucially, the shell of hydrogen gas surrounding the now-contracting core.
When this surrounding hydrogen shell reaches a sufficiently high temperature and density, hydrogen fusion ignites in the shell. This hydrogen shell burning is often even more intense than the previous core burning, causing the star’s outer layers to expand dramatically, transforming it into a red supergiant. Stars like Betelgeuse (M2Iab, previously mentioned in the H-R diagram context - first part) are prime examples of this stage.
Meanwhile, the helium core continues its relentless contraction and heating.
When its temperature reaches approximately 100 million Kelvin (10⁸ K), helium nuclei (alpha particles) can overcome their greater electrostatic repulsion compared to protons.
At this point, helium fusion ignites in the core, primarily through the triple-alpha process:
$$ 3\ (^{4}\mathrm{He}) \rightarrow {}^{12}\mathrm{C} + \gamma + 7.275\ \text{MeV} $$
This process converts three helium nuclei into one carbon nucleus, releasing energy that once again provides outward thermal pressure, temporarily halting the core’s contraction and establishing a new, albeit shorter-lived, hydrostatic equilibrium.
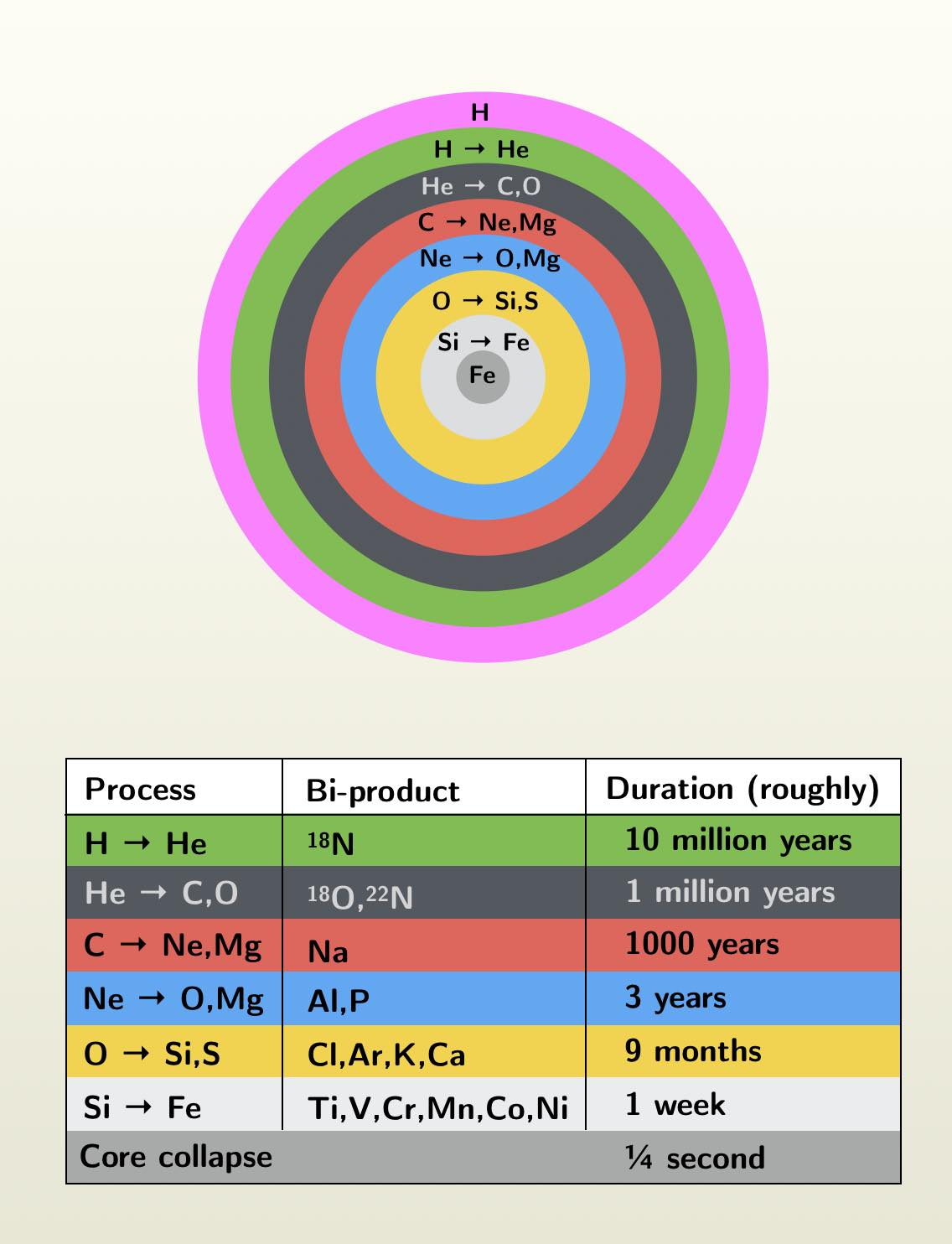
The Onion-Skin Structure and Lifespan of a Massive Star (reference)
This process converts three helium nuclei into one carbon nucleus, releasing energy that once again provides outward thermal pressure, temporarily halting the core’s contraction and establishing a new, albeit shorter-lived, hydrostatic equilibrium.
As the helium fuel in the core is depleted, gravity once again dominates, causing the carbon-rich core to contract and heat further. This triggers a sequential series of burning stages in concentric shells around the core, forming a distinct onion-skin structure.
Each stage requires progressively higher temperatures and pressures to overcome the increasing Coulomb barrier (refer part 1) between the heavier, more highly charged nuclei, as roughly indicated by $ ( k_B T \gtrsim \frac{Z_1 Z_2 e^2}{4 \pi \varepsilon_0 r} ) $ where $ (Z_1 Z_2) $ increases with heavier elements.
Carbon burning
At temperatures around 5×10⁸ K, carbon nuclei fuse to produce heavier elements such as Neon (Ne), Sodium (Na), and Magnesium (Mg). This stage can last for a few thousand years.
$$ {}^{12}\mathrm{C} + {}^{12}\mathrm{C} \rightarrow {}^{20}\mathrm{Ne} + {}^{4}\mathrm{He} $$
or
$$ {}^{12}\mathrm{C} + {}^{12}\mathrm{C} \rightarrow {}^{23}\mathrm{Na} + {}^{1}\mathrm{H} $$
Neon burning
Once carbon is exhausted, the core contracts until it reaches roughly 10⁹ K. Neon nuclei photodisintegrate (break apart by high-energy gamma rays), producing oxygen and helium, which then fuse further. This phase is much shorter, typically lasting only a few years.
$$ {}^{20}\mathrm{Ne} + \gamma \rightarrow {}^{16}\mathrm{O} + {}^{4}\mathrm{He} $$
followed by
$$ {}^{20}\mathrm{Ne} + {}^{4}\mathrm{He} \rightarrow {}^{24}\mathrm{Mg} + \gamma $$
Oxygen burning
At even higher temperatures (around 2×10⁹ K), oxygen nuclei fuse to form elements like Silicon (Si), Phosphorus (P), and Sulfur (S). This stage might last only months.
$$ {}^{16}\mathrm{O} + {}^{16}\mathrm{O} \rightarrow {}^{28}\mathrm{Si} + {}^{4}\mathrm{He} $$
Silicon burning
The final stage of fusion occurs at core temperatures exceeding 3×10⁹ K. Silicon nuclei fuse into elements up to Iron (Fe) through a complex chain of reactions involving alpha particle capture. This stage is extremely rapid, potentially lasting only a day for a very massive star.
$$ {}^{28}\mathrm{Si} + {}^{4}\mathrm{He} \rightarrow {}^{32}\mathrm{S} + \gamma $$
followed by successive captures such as
$$ {}^{32}\mathrm{S} + {}^{4}\mathrm{He} \rightarrow {}^{36}\mathrm{Ar} + \gamma $$
eventually producing isotopes up to iron-group nuclei.
The duration of each burning stage dramatically shortens because the energy yield per unit mass for heavier element fusion is lower, and the star’s luminosity remains extremely high. Throughout this entire post-main-sequence evolution, the star is still primarily supported by the thermal pressure generated by these various nuclear fusion reactions occurring in the core and surrounding shells. The outward flow of energy generated by these processes continuously balances the inward pull of gravity. However, this chain of energy generation reaches end at some point, leading to the star collapse.
End of Fusion
The sequential burning of elements in a massive star’s core ceases when silicon fusion culminates in the production of iron (specifically, Iron-56, ⁵⁶Fe).
For all elements lighter than iron, nuclear fusion is an exothermic process (means fusing these nuclei releases energy). This energy release occurs because the product nucleus has a higher nuclear binding energy per nucleon (protons and neutrons) than the initial fusing nuclei. For instance, fusing hydrogen into helium releases approximately ∼7 MeV per nucleon. This surplus binding energy is converted into kinetic energy and photons, which contribute to the star’s thermal pressure and luminosity.
However, Iron-56 possesses the highest nuclear binding energy per nucleon of all known atomic nuclei. This means that any nuclear reaction involving iron — whether trying to fuse it into heavier elements or attempting to fission it into lighter ones, would absorb energy (endothermic) rather than release it. The system would require energy input to proceed, violating the core’s ability to self-sustain fusion.
Once the core of a massive star is predominantly iron, the star can no longer extract energy from nuclear fusion. This leads to the collapse due to the excess outward gravitational pull.
Electron Degeneracy Pressure
With the end of fusion in the iron core, gravity begins to assert its dominance, causing the core to rapidly contract. As the density of the core skyrockets, the particles within it are squeezed ever closer. At these extreme densities, a new form of pressure, rooted in the principles of quantum mechanics, begins to emerge: electron degeneracy pressure (EDP).
Imagine trying to pack countless electrons into an incredibly small volume. As the density increases, all the available low-energy quantum states become filled. Due to the Pauli Exclusion Principle, any additional electrons attempting to occupy this space are forced into higher and higher energy states, even if the temperature is close to absolute zero. The collective kinetic energy of these tightly packed, high-energy electrons creates an immense outward pressure that resists further compression. This pressure, entirely independent of temperature, is electron degeneracy pressure (EDP).
The magnitude of EDP is directly related to the density $ \rho $ of the electron gas.
For non-relativistic electrons:
$$ P_\text{EDP} \propto \rho^{5/3} $$
As densities increase further and electrons become relativistic [their speeds approach $( c )$] , the pressure dependence changes to:
$$ P_\text{EDP} \propto \rho^{4/3} $$
For a brief, critical moment during the core collapse of a massive star, electron degeneracy pressure provides a powerful, albeit ultimately insufficient, outward force, temporarily resisting the inward pull of gravity. This pressure is the same force that stabilizes white dwarfs, stellar remnants of less massive stars.
For a core supported solely by electron degeneracy pressure, there’s an upper mass limit known as the Chandrasekhar Limit, approximately 1.4 $ M_\odot $ (1.4x mass of Sun). Above this limit, where relativistic effects become dominant, EDP is no longer strong enough to counteract gravity.
Catastrophic Core Collapse
For the iron core of a massive star, whose mass typically exceeds the Chandrasekhar Limit (e.g., 1.5–2.0 $\ M_\odot\ $), electron degeneracy pressure provides only a fleeting reprieve. The sheer strength of gravity, combined with further physical processes, quickly overcomes this quantum resistance.
As the core continues its rapid collapse, two critical phenomena occur:
-
Neutronization (Electron Capture)
With densities reaching approximately $ 10^{10} \ \text{kg/m}^3 $ (a thousand tons per cubic centimeter), the electrons are forced to combine with protons, forming neutrons and emitting energetic neutrinos $ ( \nu_e ) $:
$$ e^- + p^+ \rightarrow n + \nu_e $$
This process, known as neutronization or electron capture, is catastrophic for electron degeneracy pressure. It removes the very particles (electrons) responsible for providing the outward quantum support, dramatically accelerating the collapse. The neutrinos, though weakly interacting, carry away enormous amounts of energy from the core, on the order of $ \ 10^{46} \ \text{joules} \ $, further contributing to the energy deficit.
-
Photodisintegration
The extreme temperatures and densities (exceeding $ \ 10^{10} \ \text{K} \ $ and $ \ 10^{12} \ \text{kg/m}^3 \ $) within the collapsing core generate high-energy gamma-ray photons. These photons are energetic enough to break apart the iron nuclei into lighter elements, and even further into individual protons and neutrons:
$$ {}^{56}\mathrm{Fe} + \gamma \rightarrow 13 {}^{4}\mathrm{He} + 4n $$
$$ {}^{4}\mathrm{He} + \gamma \rightarrow 2p + 2n $$
Both of these reactions are highly endothermic; they absorb immense amounts of energy (e.g., 124 MeV to break down a single Iron-56 nucleus) from the core, further reducing the internal pressure and cooling the core, which intensifies the gravitational collapse.
With electron degeneracy pressure removed and energy being absorbed rather than generated, the core implodes without resistance. This is an incredibly rapid event, occurring in just milliseconds. The inner core, initially Earth-sized, shrinks to a mere tens of kilometers in diameter, approaching densities greater than that of an atomic nucleus. The speed of this implosion can reach a significant fraction of the speed of light.
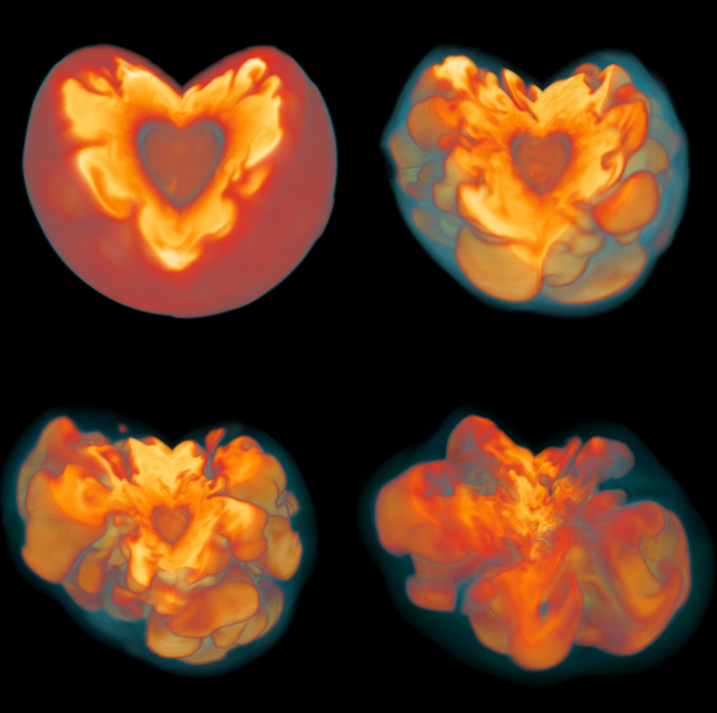
snapshots showing the boiling of the neutrino-heated region around the nascent neutron star. (reference)
Type II Supernova
The catastrophic collapse of the iron core does not end quietly. When the inner core reaches nuclear densities (around $ 10^{17} \text{kg/m}^3 $, comparable to that of an atomic nucleus), the strong nuclear force, which usually holds nuclei together, becomes strongly repulsive at these incredibly short distances. This effectively makes the core incompressible.
The infalling outer layers of the core, still plummeting inward at relativistic speeds, violently collide with this suddenly stiff, super-dense neutronized inner core. This collision creates a powerful outward-propagating shockwave.
Initially, the shockwave struggles to move through the infalling material. However, the immense pressure of neutrinos generated during neutronization, carries away vast amounts of energy from the core. While most neutrinos escape, a small fraction (about 1%) interact with the material behind the stalled shockwave, re-energizing it and driving the shockwave powerfully outward. This re-energized shockwave blasts through the remaining stellar material.
As the shockwave propagates outward, it heats the stellar envelope to extreme temperatures and pressures. In this turbulent, energetic environment, a burst of rapid nuclear reactions occurs, such as the r-process (rapid neutron capture). Here, existing atomic nuclei quickly absorb a large number of free neutrons (produced during core collapse and by the shockwave), creating many of the elements heavier than iron, such as gold, platinum, and uranium, which cannot be formed in the star’s normal, hydrostatic burning stages.
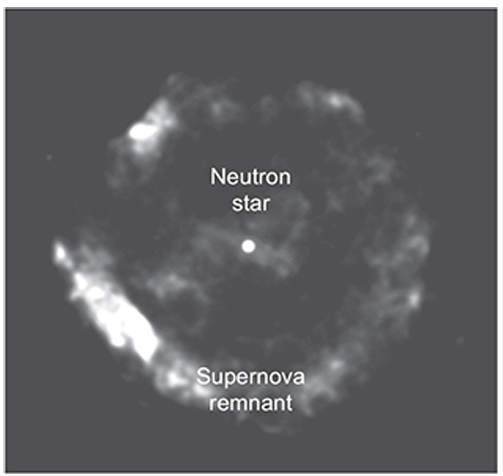
Neutron Star and Supernova Remnant (reference)
This expulsion of the star’s outer layers, is what we observe as a Type II Supernova. For a brief period, the supernova can shine brighter than an entire galaxy, with a peak optical luminosity of about $ 10^{36} \text{W} , \ 10^9 L_\odot $, but radiating total energy on the order of $ 10^{44} \ \text{joules} $ in light and kinetic energy, and vastly more ($ \sim 10^{46} \ \text{joules} $) in neutrinos.
Further…
Neutron star and Black holes